Основные дидактические функции задач по теме "Площади фигур" и их реализация в учебном процессе

Следует обратить внимание учащихся, что заштрихованный треугольник (рис.32) составляет половину площади как одного, так и другого параллелограмма. А это и означает, что их площади равны.

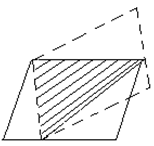
Рис.32

Это довольно нестандартный подход к решению задач, но его краткость и удивительная простота действительно восхищают учащихся, что естественно повышает их интерес к изучению геометрии.

Говоря о реализации развивающей и воспитательной функциях задач "на площади", нельзя не сказать о различных задачах на разрезание и перекраивание фигур, конструироании из бумаги. Подобные задачи призваны повысить интерес учащихся к геометрии, развивать их фантазию, творческие возможности. Кроме того, можно смело сказать, что решение подобных задач вносит определенный вклад в художественное воспитание учащихся, в развитие у них изобразительной культуры. Применять такие задачи можно и на уроках, и во внеклассной работе, для этого в сборнике представлено достаточное количество подобных задач. Приведем пример задачи на конструирование из бумаги.

Задача. 1) Укажите площадь данного на рис.33 квадрата, считая одну клетку за 1 кв. ед.

2) Вырежьте этот квадрат из бумаги и сложите из него треугольную пирамиду (рис.34);

3) Найдите площадь полной поверхности полученной пирамиды.

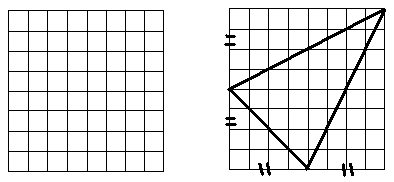
Рис.34

Данное задание не только на измерение площади квадрата, его выполнение осуществляет пропедевтику курса стереометрии, а именно знакомит учащихся с пространственным телом и площадью его поверхности. Подобные задания развивают пространственные представления учащихся и демонстрируют, что тема "Площади фигур" находит свое применение не только среди плоских фигур, но и среди пространственных тел. Подобные задачи можно предложить учащимся уже в 5-6 классах (вместо пирамиды можно сначала взять куб, цилиндр).

Выше уже отмечалась возможность применения задач "на площади" сборника при организации внеклассной работы (в приложении приведен пример игры на внеклассном мероприятии). Сборник оснащен и довольно трудными задачами, которые целесообразно применять при организации кружковой работы, факультативов или предлагать их для решения сильным ученикам.

Итак, мы показали, как задачи "на площади" сборника служат основным дидактическим целям, а именно: формируют системы знаний, умений и навыков решения различных типов задач, творческое мышление учащихся; способствуют развитию интеллекта, мировоззрения, нравственных качеств, стимулируют развитие интереса к геометрии, выполняют познавательную роль в обучении. Решение этих задач способствует развитию мышления школьников, а это, пожалуй, самая важная цель обучения математике.

Опытная проверка разработанных материалов и анализ результатов

Опытная проверка задач предлагаемого сборника проводилась в ЦО № 654 города Москвы и охватила 45 учеников восьмых классов: 8 "МиФ" и 8 "БиХ" ("МиФ" – это класс с физико-математическим уклоном, а "БиХ" – с биолого-химическим). Цели проведенной проверки состояли в следующем:

1) Получения экспертной оценки учителей математики, в которую входили:

Проверка целесообразности применения задач предлагаемого сборника;

Оценка варианта типологии задач, предложенной в работе;

Возможности применения задач сборника;

Возможные формы организации деятельности учащихся при работе с предложенными задачами;

Уровень доступности задач для учащихся различных категорий.

2) Разработка проверочной работы по теме "Площади фигур" с целями:

Проверки остаточных знаний учащихся по данной теме;

Урок-изучение нового материала
Тема: Структура прозвища. Цель: сформировать умение выделять основные структурные типы прозвищ. Оборудование: запись на доске. Ход урока: I. Организационный момент. II. Постановка целей урока. Ребята, сегодня на уроке нам предстоит познакомиться с основными структурными типами прозвищ, а также прон ...

Методы и приемы формирования умственной активности детей дошкольного возраста
Одним из приемов формирования умственной активности дошкольников является дидактическая игра, в которой одновременно действуют два начала: учебное, познавательное и игровое, занимательное. Это обусловлено потребностью смягчения перехода от одной ведущей деятельности к другой, а также тем, что в про ...

Описание компетенции ПКНО-4
Федеральный образовательный стандарт предусматривает, что выпускник должен обладать профессиональными компетенциями в образовательной деятельности на начальной ступени общего образования (ПКНО). Компетенция ПКНО-4 определяется как "готов создавать условия, облегчающие адаптацию детей к учебном ...