Основные дидактические функции задач по теме "Площади фигур" и их реализация в учебном процессе

Выше на примере площади трапеции уже приводился пример доказательства теоремы различными способами. Также различными способами можно доказать и теорему о площади параллелограмма, треугольника. Многие задачи предлагаемого сборника задач подразумевают наличие нескольких решений, а значит они реализуют развивающую функцию задач "на площади". Но задачи сборника были подобраны и с учетом реализации ими воспитательной функции задач "на площади", а именно направленных на формирование эстетического вкуса учащихся, повышения уровня математической культуры школьников. Ведь решение задач различными способами – это первый шаг к пониманию и восприятию внутренней красоты задачи. Приведем примеры задач, направленных на формирование и развитие эстетического вкуса учащихся, которые можно предложить решить различными способами, по теме "Площади фигур", поскольку эта тема является наиболее привлекательной для учащихся с эстетической точки зрения, к тому же ко времени изучения данной темы у учеников имеется определенный запас теоретических знаний, и они могут применить на практике полученные знания при поиске различных способов решения с целью отыскания наиболее рационального, красивого.

Задача. По данным рис.23 найдите площадь заштрихованной фигуры:

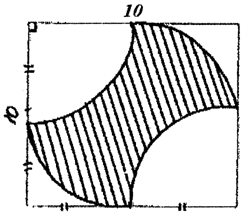
Решение.

1-ый способ. (рис.24 )

S = 102-2S1-2S2

S1 = (100-25π ) = 25-

S2 = *25π =

S = 100-2(25-+) = 50

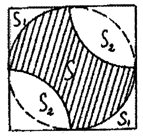
Рис.24

2-ой способ. (рис.25)

S = 102-(5)2 = 50

Рис.25

3-ий способ. (рис.26 )

S = 2*52 = 50 или S = = 50

Рис.26

4-ый способ. (рис.27 )

S = 2*52 = 50

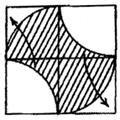
Рис.27

5-ый способ. (рис.28 )

S = = 50

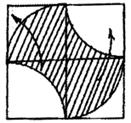
Рис.28

Данная задача представляет интерес не только с точки зрения различных способов решения, но и условие ее привлекает своей эстетической стороной. Приведенная задача побуждает учеников к математическому творчеству, поиску новых решений. Таких задач представлено в данном сборнике достаточное количество, что позволяет использовать его на уроках геометрии в целях развивающего обучения. Если на уроке предусмотрено решить задачу несколькими способами, то при этом полезно разбить класс на группы и предложить каждой группе решить задачу определенным способом, дав направление поиска. Сначала это может быть небольшая подсказка учителя, например, решить задачу или доказать теорему, используя определенное свойство геометрического объекта, выполнить дополнительное построение и т.п. Затем, решив задачу, разумно поставить перед учащимися вопрос "Нельзя ли получить тот же результат иначе?". После того, как ученики решили задачу различными способами, разумно будет разобрать достоинства и недостатки каждого способа решения с целью выбора наиболее оптимального с точки зрения школьников. При этом учащиеся учатся оценивать решение задачи, искать нестандартные подходы к решению, видеть и оценивать эстетическую сторону решения задачи, что, несомненно, положительно влияет как на развитие познавательного интереса школьников, так и на развитие мышления учащихся и их общей культуры.

Организация поисковой деятельности ученика в работе В.В. Давыдова «Проблемы развивающего обучения»
Общепринятая в современной общеобразовательной школе форма организации учебного процесса в виде групповой работы учащихся под руководством учителя (классно-урочная система) справедливо вызывает нарекания со стороны педагогов-теоретиков и учителей-практиков. Изобретённая в своё время Я.А. Коменским ...

Роль педагогической практики в формировании у будущих учителей психолого-педагогических и методологических навыков
география педагогический практика методологический Содержание психолого-педагогической практики с учетом современных принципов обучения и воспитания, носит интегративный характер и предполагает: ознакомление с учебно-воспитательной работой школы; изучение личности и коллектива; воспитательную работ ...

Особенности применения принципа системности и систематичности
Одним из принципов, трактующим о содержании учебной деятельности и раскрывающим её предметную основу, является принцип системности и последовательности. В традиционном плане он содержит очень важное требование логичности, последовательности и преемственности, когда каждое последующее знание или уме ...