Основные дидактические функции задач по теме "Площади фигур" и их реализация в учебном процессе

Задание №2 в обоих вариантах вызвало некоторые затруднения. Оно и понятно, ведь ребята только приступили к изучению темы "Синус", но уже знали какие накладываются ограничения на синус. Формула площади треугольника, выраженная через две стороны и синус угла между ними, была сообщена учащимся непосредственно перед работой. При решении этого задания ребятам нужно было проявить смекалку и внимание, и многие с этим успешно справились. Если снова сравнивать результаты обоих классов между собой, то здесь ситуация следующая: в первом варианте результаты лучше у 8 "БиХ", а во втором – у 8 "МиФ".

В задании №3 обоих вариантов нужно было найти пары равновеликих треугольников в параллелограмме и в трапеции. Это задание было направлено на внимание, а также на знание ребятами необходимого теоретического материала (учащиеся не увидели треугольники с равными основаниями и одинаковой высотой). Многие школьники не увидели все пары равновеликих треугольников в параллелограмме, а ведь в основе этого задания лежало важное свойство медианы треугольника. Кстати, с этим заданием в явном виде справились практически все ученики первого варианта (задание №5). Случай с трапецией оказался для учеников проще – многие увидели единственную нужную пару из списка предложенных. Оба класса в этом задании проявили одинаковые успехи.

Задание №4 было на использование формулы площади круга, которую ребята будут изучать только в середине 9 класса. Здесь ребятам пригодились те знания, которые они приобрели в младших классах средней школы. Приятно удивило то, что практически все ученики обоих классов успешно справились с этим заданием.

Задание №5 в первом варианте было направлено на проверку знания учащимися важного, полезного для решения многих задач (например, №3 первого варианта) теоретического факта, что медиана треугольника делит его площадь пополам. Во втором варианте задание также теоретического содержания – на понятие равновеликости фигур.

И, наконец, последнее задание в обоих вариантах было на применение площадей к решению задач, а именно на метод площадей. С этим заданием практически не было проблем, а это значит, что учащиеся успешно применяют метод площадей при решении задач.

На следующем уроке с учащимися был проведен разбор ошибок проверочной работы, а также им было предложено высказать свое мнение о каждой задаче данной работы. Большинство ребят посчитало интересными задачи №2, №3, №5, легкими - №4, №6 и полезными - №1, №5 и №6.

В конце урока ребятам было предложено как необязательное задание порешать понравившиеся из 14 задач по теме "Площади фигур", на что большинство учащихся с охотой согласились. А задачи были следующие:

№1. Данный треугольник "перекроить" в прямоугольник (рис.41).

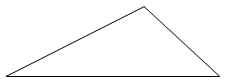
Рис.41

№2. По данным рис.42, 43 найдите площади заштрихованных фигур:

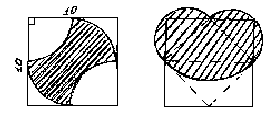
Рис.43

№3. Докажите, что площадь черной фигуры равна сумме площадей белых фигур (рис.44):

№4. Основания AB и CD трапеции ABCD соответственно равны a и b, O – точка пересечения диагоналей (рис.45). Найдите отношение площадей треугольника AOB и трапеции ABCD.

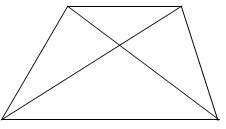
Рис.45

№5. Вершины квадрата соединены с серединами его сторон, как показано на рис.46. Во сколько раз площадь внутреннего квадрата меньше площади исходного?

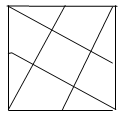
Рис.46

№6. Точка, взятая внутри равностороннего треугольника, соединена со всеми его вершинами. Кроме того, из нее опущены перпендикуляры на все стороны треугольника. Три из образовавшихся шести треугольников через один заштрихованы (рис.47). Докажите, что сумма площадей заштрихованных треугольников равна сумме площадей незаштрихованных треугольников.

Возрастные особенности эмоционально-ценностного компонента у младших школьников
Возрастное развитие человека - это непрерывный процесс самоизменения, каждый этап которого связан с ведущим видом деятельности, проходит в определенной социальной ситуации развития и характеризуется появлением новых психических новообразований и изменением личности. Динамика перехода от одного возр ...

Понятие «личность», «индивидуальность», «индивид»
Личность - одна из базовых категорий психологической науки. Для того чтобы понять, что такое личность, и выделить основные свойства, позволяющие описать психический склад личности, необходимо рассмотреть это понятие в ряду "индивид - субъект деятельности - личность - индивидуальность", пр ...

Проблема подготовки детей к обучению математике в школе
Далеко не все дошкольники подходят к обучению в школе с необходимым багажом математических знаний или близких к ним. Нередко дефицит соответствующей работы со стороны родителей и педагогов приводит к тому, что будущий первоклассник не умеет выделять и сравнивать признаки различных предметов и явлен ...