Упражнения и методические рекомендации для подготовки учащихся к сдаче заданий уровня А

Ответ: 2.

Второе решение. Известно, что если a≥0, b≥0, то . При этом равенство достигается в том и только в том случае, если . Тогда . В нашем случае равенство достигается только при . При х=0 функция принимает наименьшее значение. Отсюда получаем, что наименьшее значение исходной функции равно 2 и достигается оно при х=0.

Третье решение. Перепишем формулировку, заданную функцию следующим образом: 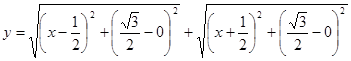. В декартовой системе координат рассмотрим точки 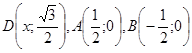. Тогда

1)

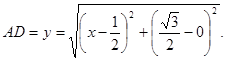
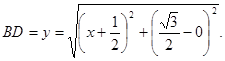
2) Точка D расположена на прямой .

З) Значение исходной функции равно сумме расстояний AD+BD.

В таком случае все сводится к решению известной геометрической задачи: на прямой СD найти такую точку D, чтобы сумма расстояний АD+ВD была наименьшей.

Для решения отображаем А симметрично относительно СD. Обозначим новую точку Теперь соединим точки В и . Расстояние B и будет наименьшим. Так как АВ=1, А, то При этом легко доказать, что прямая B проходит через точку С.

Четвертое решение. Для определения наименьшего значения применим производную: .

Найдем критические точки: .

Комментарий.

Решая данное уравнение, получаем, что х=0. Исследовав значения производной, приходим к выводу, что в этой критической точке – наименьшее значение функции.

Теперь видно, что стандартное исследование поведения функции по производной достаточно сложно (попробуйте его реализовать). Поэтому подготовка учащихся к ЕГЭ должна предусматривать обучение поиску наибольшего и наименьшего значений без производных (это должно проводиться в 8–10 классах).

Задание 7.

Найдите наименьшее значение функции .

Решение. Сразу видно, что применение производной приведет к серьезным осложнениям. Поступим иначе. Рассмотрим функции и . Легко убедиться, выделяя квадрат подкоренного выражения и учитывая свойство монотонности функции , что первая функция имеет наименьшее значение при х=1. Так как при всех х, то вторая функция имеет наименьшее значение 0, и оно достигается при , т.е. при х=1+2n, . Среди чисел вида х=1+2n, содержится число 1. Отсюда следует, что функции и принимают свои наименьшие значения при х=1. Следовательно, исходная функция принимает наименьшее значение при х=1. .

Педагогика со времени монгольского ига и до Петра Великого в Московской Руси
В таком положении было просвещение русского народа до нашествия монголов (до середины XIII в). Последнее особенно сильно отразилось на Северо-Восточной Руси, и с этих пор история Северо-Восточной и Юго-Западной Руси идет различными путями. Монгольское иго содействовало упадку и без того, как мы уже ...

Основные подходы к проблеме самостоятельной лингвистической подготовки студентов-переводчиков
Основная задача высшего образования заключается в формировании творческой личности специалиста, способного к саморазвитию, самообразованию, инновационной деятельности. Решение этой задачи вряд ли возможно только путем передачи знаний в готовом виде от преподавателя к студенту. Происходящая в настоя ...

Метод показа
Метод показа (анализа) - важный экскурсионный метод. Ведь весь смысл выхода за пределы класса, школы и заключается в том, чтобы учащиеся приобрели знания в ходе наблюдения объектов, расположенных в естественной обстановке или собранных в залах музея. У школьников, особенно младших классов, развито ...