Психолого - дидактические основы обучения по теме "Площади фигур"

Легкость запоминания зависит от количества запоминаемого. Необходимо стараться уменьшать количество материала, подлежащего заучиванию. При выводе формул, правил, доказательстве теорем достаточно понять и запомнить только идею, лежащую в основе рассуждения. Так, например, зная формулу площади параллелограмма, выраженную через диагонали параллелограмма и синус угла между ними, можно получить формулу площади ромба и квадрата, использовав тот теоретический факт, что диагонали ромба и квадрата пересекаются под прямым углом, а значит, синус угла между диагоналями равен единице.

Прочность вычислительных навыков в значительной степени зависит от числа упражнений, выполненных учащимися. Тема "Площади фигур" как раз предполагает решение как можно большего числа различных задач. Учителю следует помнить при составлении системы упражнений, что быстрый переход от решения простых примеров к сложным отрицательно влияет на прочность усвоения. Важно учитывать, что при первичном закреплении необходимо решать множество задач на прямое применение изученных знаний, и совсем не следует сразу стремиться сложные решать задачи, комбинированного типа, в которых изученное действие встречается крайне редко. При этом полезно решать задачи такого типа:

Задача: На рис. 12 изображен треугольник.

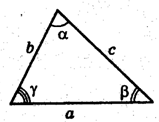
Рис.12

Заполните пропуски в следующей таблице:

Большое значение для формирования прочных знаний имеет повторение пройденного. В ряде случаев повторение органически связывается с изучением нового материала, так как обусловлено логической взаимосвязью изучаемых и изученных положений.

Принцип активности

Обучение должно опираться на активную, творческую работу школьника. Принцип активности прежде всего осуществляется в ходе уроков. Одна из наиболее распространенных форм урока – живая беседа между учителем и учениками. Учащимся задаются вопросы, задачи, примеры. Ответы составляют содержание нового материала. Живая беседа – одна из форм активного изучения. Наряду с ней применяется изучение материала в процессе упражнений. В практике преподавания получили распространение и другие формы осуществления принципа активности. К ним, в частности, относится такая методика проведения опроса и проверки домашнего задания, при которой все учащиеся напряженно следят за ответами товарищей, подмечают и исправляют ошибки в ответах, вносят дополнения. Опытные учителя придают большое значение развитию творческой инициативы школьников. Учащиеся делают рефераты, доклады, сообщения, выпускают газеты. Темами рефератов могут служить вопросы, связанные с углубленным изложением программы, вопросы из истории математики и т.п. Например, при изучении темы "Площади фигур" полезно приготовить учащимся сообщения из истории зарождения теории площадей, о возникновении системы мер, о древних способах вычисления площадей различных плоских фигур и т.д.

Постановка докладов и рефератов, выпуск газет, проведение олимпиад повышает интерес учащихся к занятиям математикой. Создание интереса к предмету – одно из условий осуществления принципа активности: интерес побуждает ученика к самостоятельным занятиям и самостоятельным поискам решений задач и ответов на вопросы.

Ведь дать каждому ученику глубокие и прочные знания – задача, требующая постоянного совершенствования собственных знаний учителя и серьезного продумывания всех элементов учебного процесса. Все усилия учителя, однако, могут оказаться бесплодными, если первым помощников в решении этого вопроса не будет сам ученик. Основной стимул учения – интерес к занятиям, и он должен систематически развиваться у каждого ученика. Для решения этого вопроса очень важна общая атмосфера в школе. Большое значение при этом имеет внеклассная работа. Однако главным условием формирования познавательной активности школьников является содержание и организация урока. Отбирая материал и продумывая приемы, которые будут использованы на уроке, учителю надо оценивать из и с точки зрения возможности возбудить и поддержать интерес учащихся к предмету. Каждый учитель знает, что класс не представляет собой однородную массу. Безусловно, имеется какая-то часть учащихся, у которых интерес к математике зародился еще до ее изучения. Таким ученикам нужны разнообразные и более сложные задачи, однообразные упражнения их утомляют. Во время выполнения упражнений тренировочного характера для них всегда надо иметь в запасе более сложные задания. Включение в домашние задания необязательных упражнений тоже в основном рассчитано на них. Но такие упражнения неободимо давать не только этим ребятам, но и всем желающим. Ведь важно привлечь к решению этих задач как можно больше учащихся. Даже среди желающих решить задачу подчас не все могут это сделать (опытная проверка это подтвердила). К тому же из-за недостатка времени организовать проверку таких задач на уроке невозможно. Решение этого вопроса может оказаться следующим: в классе делается специальный стенд, где вывешивается сначала текст необязательного задания, а через некоторое время и его решение. Причем решение вывешивается тогда, когда ребята сдали на проверку учителю свои работы. Кроме того, решения у учащихся могут быть самыми разнообразными и некоторые из них, естественно, верно решенные, могут оказаться на этом стенде. В некоторых случаях на стенде помещаются рисунки, по которым можно "додумать" решение. Например, в 8 классе после изучения темы "Площадь многоугольника" учащимся можно предложить в качестве необязательной задачу на доказательство (рис.13), а через неделю помещался только рисунок к ее решению (рис.14).

Характеристика функций речи
Речь во всем ее многообразии, является необходимым компонентом общения, в процессе которого она и формируется. Важнейшей предпосылкой совершенствования речевой деятельности дошкольников является создание эмоциональной благополучной, благоприятной ситуации, способствующей возникновению желания актив ...

Анализ педагогических подготовок к формированию знаний учащихся
Основная структурная единица педагогического процесса - классный урок. В нем концентрируются все элементы обучения и воспитания, обусловливается их непрерывная динамика и последовательное положительное воздействие на учащихся. Педагогическая сущность и образовательное воздействие урока проявляется ...

Предпосылки, обусловленные личностью Л.Н. Толстого
толстой педагогическая обучение ясная поляна В одном из номеров журнала "Ясная поляна" за 1862 год была размещена статья открывавшаяся следующим вопросом: "Что стоит теперь на первом плане у всех наших деятелей мысли и слова?" [1] Ответом был народ. Народ, которому все желали пр ...