Психолого - дидактические основы обучения по теме "Площади фигур"

Критерием сознательности является и речь учащихся. Неточные формулировки свидетельствуют о непонимании материала и нередко выражают ошибочные утверждения. Например, ученик, пропустивний слова: "проведенную к этой стороне" в формулировке теоремы "Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне" делает неверное заключение. Учителю следует воспользоваться такого рода ошибкой, чтобы обратить внимание учащихся на значение точности речи.

Принцип наглядности

В преподавании математики нагдядность применяется как средство, способствующее правильному формированию математических понятий, облегчающее изучение материала, развивающее пространственные представления и воображение учащихся. Наглядность – основа прочности знаний.

При решении задач и доказательстве теорем учащиеся рассматривают геометрические фигуры в самых разнообразных положениях. Если учитель, вводя понятие, не вариировал форму и размеры чертежа, а также его положение на доске, то учащиеся не узнают определенный геометрический образ, когда он изображен в непривычном для них положении. Аналогичная ситуация происходит при замене одних обозначений другими. В этих случаях многие учащиеся испытывают некоторые затруднения при использовнии формул для вычисления площадей фигур и т.д. Эти затруднения можно предотвратить, если при введении понятия не ограничиваться построением одного чертежа.

Наглядность в обучении математике выступает как средство, облегчающее изучение материала. Материал легче усваивается учащимися, когда объяснение учителя сопровождается применением наглядных пособий. В геометрии, например, чертеж помогает ученику провести рассуждения при доказательстве теоремы, так как отдельные этапы доказательства ученик может связать с наглядными геометрическими образами. В процессе построения надо обратить внимание учащихся на особенности чертежа, вытекающие из условия теоремы (задачи). Правильно выполненный чертеж помогает понять содержание задачи (теоремы) и найти способ ее решения (доказательства). Полезен следующий прием.

Общий прием построения чертежа по условию задачи (теоремы)

Выполняйте чертеж аккуратно, не обязательно по всем правилам черчения, но примерно их придерживаясь (прямой угол должен выглядеть прямым углом, середина отрезка – серединой и т.п.), большим и "просторным";

Не перегружайте чертеж; иногда полезно изобразить лишь "функционирующие" части геометрической фигуры (например, если нужно найти радиус окружности, то саму окружность целиком можно не изображать);

Уточняйте чертеж по мере решения задачи, пытайтесь изобразить все возможные конфигурации, отвечающие условию и ходу решения задачи (лишние потом можно отбросить);

Например, к задаче "доказать, что R – радиус описанной около треугольника окружности равен , где a, b, c – длины сторон данного треугольника" возможны следующие варианты выполнения чертежа (рис.6):

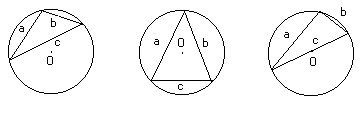
Рис. 6

Используйте дополнительные построения, облегчающие решение (вводящие новые углы, отрезки и т.п.);

В то же время избегайте чрезмерного усложнения чертежа; этого можно достигнуть за счет "выносных чертежей", изображающих отдельные фрагменты всей фигуры;

Полезно непосредственно на чертеже указывать известные числовые и буквенные значения величин (отрезков, углов), заданных в условии или полученных в процессе решения;

Если в задаче говорится о фигурах общего вида (например, о произвольном треугольнике, четырехугольнике и т.п.), то нельзя изображать их как частные случаи (так, произвольный треугольник не должен выглядеть прямоугольным или равнобедренным, а произвольный четырехугольник – параллелограммом и т.п.).

Такое ошибочное выполнение чертежа приводит к построению неверных гипотез и умозаключений.

Важно помнить, что правильно выполненный чертеж помогает понять условие теоремы, выдвинуть гипотезу о ее доказательстве, но ни в коем случае не является самим доказательством.

Говоря о значении наглядности как средстве, облегчающем усвоение материала, следует подчеркнуть, что всякая переоценка роли наглядных пособий может принести даже вред развитию мышления и воображения учащихся. Так, пространственное воображение учащихся будет развиваться слабее, если решение каждой задачи и доказательство каждой теоремы учитель станет разъяснять на модели. Поэтому преподаватель должен в зависимости от конкретного материала и уровня развития учащихся решить вопрос, пользоваться наглядными пособиями или нет. Здесь можно лишь посоветовать учителю постепенно приучать учеников старших классов решать некоторые задачи, не пользуясь чертежом.

Возрастные особенности детей младшего школьного возраста
Младший школьный возраст является наиболее благоприятным для развития физических способностей (скоростные и координационные способности, способность длительно выполнять циклические действия в режимах умеренной и большой интенсивности). В возрасте 7-10 лет начинают формироваться интересы и склонност ...

Историко-педагогическая динамика процесса взаимодействия физики как учебной дисциплины и технического образования в СССР
В современных теоретических и поисковых исследованиях в области методики преподавания физики для инженерных специальностей очевиден дефицит историко-педагогического знания. Это отрицательно сказывается на основательности и надежности, разрабатываемых сегодня идей и предложений педагогических наук, ...

Система работы школы и единый государственный экзамен
Школьное математическое образование должно быть направлено в первую очередь на развитие умственных способностей школьников. Математика призвана учить школьников умению рассуждать и доказывать, приводить примеры и контрпримеры, индукции и дедукции, обобщению и конкретизации и т.д. – всему тому, без ...