Методические рекомендации по изучению функциональной линии в 8 классе

В результате изучения данного пункта школьники учатся описывать графическую ситуацию по-разному, используя геометрический, алгебраический, функциональный языки. Например: «функция у = f(x) принимает значение, равное 0, при х = –1 и х = 2», «график функции у = f(x) пересекает ось х в точках с абсциссами, равными –1 и 2», «уравнение f(x) = 0 имеет корни –1 и 2». То есть, учащиеся должны понимать эквивалентность соответствующих формулировок и свободно переходить от одной из них к другой.

В следующем пункте «Свойства функций» рассмотрены такие свойства функции:

область определения;

наибольшее и наименьшее значение функции;

нули функции;

промежутки знакопостоянства;

промежутки возрастания и убывания функции.

Цель данного пункта – это показать наглядно с помощью графиков смысл вводимых понятий. Формализация свойств функций отнесена к старшим классам. Здесь же важно, чтобы учащиеся правильно употребляли новые термины, понимали, как указанные свойства отражаются на графике, и умели по графику отвечать на вопросы, касающиеся свойств функций.

Заметим, что усвоение свойств функций и, как следствие, выполнение заданий на установление свойств функции по ее графику, традиционно вызывает трудности у учащихся. Наиболее часто ученики путают промежутки возрастания или убывания с промежутками, на которых функция принимает положительные или отрицательные значения. Параболу, ветви которой направлены вверх (вниз), многие считают графиком возрастающей (убывающей) функции. Для предупреждения подобных ошибок необходимо, чтобы свойства функций воспринимались учащимися осмысленно, а не формально. Этому может помочь обращение к содержательным графикам, например, к графику температуры. Учащимся стоит разъяснить, что как по графику температуры легко выяснить нужную информацию, так и график любой функции наглядно отражает все её свойства. Тот большой опыт работы с графиками реальных зависимостей, который приобрели учащиеся к данному моменту, поможет им перекинуть мостик от содержательных задач, связанных с графиками, к графикам произвольных функций.

Система упражнений.

Здесь содержаться упражнения, в которых по графику функции необходимо ответить на вопросы, касающиеся свойств функции, на сопоставление графиков и функциональных зависимостей; упражнения, в которых по известным свойствам функции необходимо задать формулу этой функции; упражнения на нахождение нулей функции (в ходе выполнения которых естественным образом повторяется материал, связанный с решением уравнений – линейных, квадратных, уравнений высших степеней, уравнений, решаемых на основе равенства нулю произведения). Кроме того, есть упражнения на построение графиков функций по известным её нулям (при решении таких упражнений повторяются графики зависимостей, изучавшихся в 7 классе).

Комментарии к некоторым упражнениям:

№ 740.

На рисунке 6 изображён график функции , областью определения которой является отрезок [–2; 2]. Используя график, ответьте на вопросы:

Есть ли у функции наибольшее или наименьшее значение, и если есть, то чему оно равно? При каком значении аргумента функция принимает это значение?

Укажите нули функции.

Укажите промежутки, на которых функция принимает положительные значения; отрицательные значения.

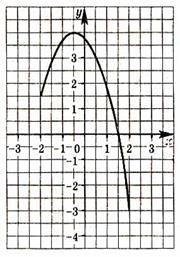Укажите промежутки, на которых функция возрастает; убывает. Рис. 6

№ 741.

На рисунке 7 изображены графики функций, определённых на множестве всех чисел. Какие свойства каждой из функций можно выяснить с помощью её графика?

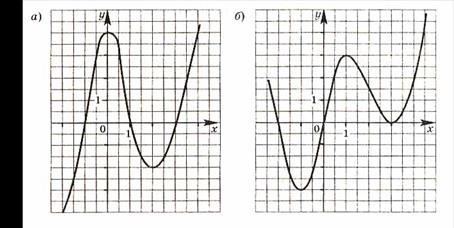Рис. 7

Учащиеся могут ошибочно подумать, что функция, график которой изображен на рис. 7 а), имеет наибольшее и наименьшее значения. В этом случае можно предложить им найти по графику какое-нибудь значение функции, большее 4 и меньшее –2. В отличие от функции на рис. 7 а), функция, график которой изображен на рис. 7 б), имеет наименьшее значение, оно равно –3.

При выполнении этого упражнения можно предложить учащимся посоревноваться: кто из них сможет указать больше свойств.

Примерный учебно-тематический план кружка по художественной обработке дерева
Таблица.1. Темы Общее кол-во часов Теоретические занятия Практические занятия Вводное занятие 2 2 — 1. Основные сведения о древесине Строение и свойства древесины Основные древесные породы Природные формы и пороки древесины Производство, сушка и хранение древесных материалов 1 1 1 2 0,5 0,5 1 1 0,5 ...

Работа по ознакомлению дошкольника с художественной литературой как средством развития театрализованной игры
Анализ психолого-педагогической литературы позволил установить, что театрализованная игра дошкольника способствует развитию психических процессов и различных качеств личности – самостоятельности, инициативности, эмоционального мира и воображения. Так же этот вид игры оказывает большое влияние и на ...

Решение логических задач как одно из средств активизации познавательной деятельности учащихся
Формировать мышление лучше всего в ходе решения задач, когда учащийся сам наталкивается на проблемы и вопросы, формулирует их и находит ответы и решения, преодолевая возникающие трудности. Задача учителя — подготовить ученика к этому, научить его приемам умственной деятельности. Графический редакто ...