Методические рекомендации по изучению функциональной линии в 8 классе

№ 710.

Дана функция 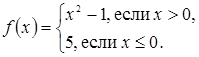Найдите значение этой функции для значения аргумента, равного –3; –2;0; 0,1; 5.

Основная трудность для учащихся – определить, в какую формулу подставлять заданные значения аргумента. Поэтому полезно сначала предложить ученикам назвать несколько значений х, для которых значение функции вычисляется по формуле , и найти значение функции для кого-нибудь из названных значений х. Затем пусть учащиеся назовут несколько значений х, для которых значение функции равно 5.

Упражнение следует выполнять подробно – для каждого из данных чисел определить, к какому из промежутков оно принадлежит и по какой формуле надо вести вычисление ( следовательно, и т.д.).

№ 711.

Дана функция 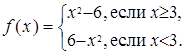Найдите значение этой функции при значении аргумента, равном:

а)

; ; ;

б) ; ; .

Это задание аналогично заданию № 710

, но в вычислительном отношении труднее. Полезно ввести подробную запись:

б)

=;

, ;

, .

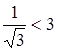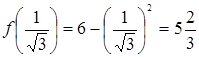№ 717.

Пусть , . Найдите:

а)

;

в)

.

Это более сложное задние на понимание символических записей, на их раскодирование. В пункте в)учащиеся фактически имеют дело со сложной функцией. Однако здесь, конечно, это понятие не вводится.

Чтобы понять смысл такой записи, как , надо просто внимательно её прочитать, а именно: значение функции f при значении аргумента, равном . Теперь ясно, как найти значение данного выражения: , .

В результате изучения пункта учащиеся должны понимать и правильно употреблять функциональную терминологию (функция, аргумент, область определения функции), записывать функциональные соотношения с использованием символического языка (). В несложных случаях выражать формулой зависимость между величинами, находить по формуле значение функции, соответствующее данному аргументу, и аргумент, которому соответствует данное значение функции.

В третьем пункте «График функции» вначале введены новые обозначения для числовых промежутков, которые уже рассматривались в 7 классе и задавались с помощью неравенств: отрезок, интервал, луч (замкнутый и открытый). Таким образом, с этого момента учащиеся могут пользоваться любым из обозначений. Например, множество чисел, больших 2, можно обозначать двумя способами: х > 2 и (2; +∞).

После этого вводится собственно материал, связанный с графиками функций. Рассматриваемые в пункте две задачи являются центральными на данном этапе изучения материала. Первая – это нахождение с помощью графика значения функции, соответствующего заданному значению аргумента, а также значений аргумента, которым соответствует данное значение функции. Вторая – это построение графиков функций по точкам.

Специфика профессиональной деятельности артиста балета
Для определения специфики профессиональной деятельности артиста балета проясним ключевые понятия и, в первую очередь – понятие «балет». Ванслов В.В. определяет балет как «вид музыкально-театрального искусства, содержание которого выражается в хореографических образах» [8, C.8]. Хореографический обр ...

Краткая характеристика эпохи Возрождения
14-15 века, вошедшие в историю под названием эпохи Возрождения, характеризуются появлением внутри феодального общества зачатков капиталистического способа производства, развитием мануфактуры и торговли, возникновением прогрессивного тогда класса- буржуазии, которая возродила культуру античного мира ...

Особенности понимания малых фольклорных форм первоклассниками
Известно, что дошкольники испытывают затруднения в понимании и интерпретировании значения пословиц и поговорок. Это подчеркивается и в исследованиях Н. Гавриш. Некоторые дети могут лишь рассказывать, о ком идет речь, например: «Это про Ваню» («Бедному Ванюшке везде камушки»), «Про Емелю, он медленн ...