Методические рекомендации по изучению функциональной линии в 8 классе

Все свойства и график функции в учебнике рассматриваются на примере конкретных функций (). По точкам строится график данной функции и вводится его название (гипербола). Из свойств выделяют только область определения, промежутки убывания и возрастания функции и делается замечание, что график данной функции не пересекает координатные оси.

Исследование проводится подробно для первого случая, когда k > 0, а для второго случая (k < 0) приведены только конечные выводы и результаты.

Традиционно построение графика обратной пропорциональности вызывает у учащихся трудности. Многие строят его небрежно, не соблюдая симметрии ветвей, ветви бывают очень короткие, очень часто в работах учащихся одна из ветвей гиперболы сначала приближается, например, к оси х, а затем удаляется от нее. Для предупреждения подобных ошибок очень важно проанализировать особенности графика, обратив внимание учащихся на то, что график состоит из двух ветвей, симметричных друг другу относительно начала координат. Каждая ветвь гиперболы по мере удаления от начала координат становится все ближе и ближе к осям, но не пересекает их. Бесконечное приближение ветвей к осям координат можно проиллюстрировать в ходе небольшого числового опыта: например, подставить в формулу вместо х несколько достаточно больших чисел в порядке их возрастания и понаблюдать, как изменяется при этом значение у. Такое мини-исследование проводится и в тексте учебника.

Система упражнений.

При выполнении упражнений повторяется весь материал, изученный в главе, – свойства функций, функциональная символика, график линейной функции.

Комментарии к некоторым упражнениям:

№ 785.

Графиком какой из функций , , является гипербола? Постройте эту гиперболу.

Учащиеся должны объяснить свой ответ, например, так: функции и являются линейными (можно попросить обосновать это утверждение), их графики – прямые. Функция – это функция вида при k = 3, графиком такой функции является гипербола.

№ 792.

Найдите координаты какой-нибудь точки, принадлежащей графику функции и находящийся от оси х на расстоянии, меньшем, чем 0,1; 0,01.

Это задание необходимо проверить на следующем уроке.

Решение.

Точки, находящиеся от оси х на расстоянии, равном 0,1, лежат на прямых .у = 0,1 и у = –0,1. Изобразив схематически график функции и прямые у = 0,1 и у = –0,1, получим, что первая прямая пересечет правую ветвь гиперболы в некоторой точке А, а вторая пересечет левую ветвь в точке В. Они будут находиться на расстоянии 0,1 от оси х. Все точки, лежащие на гиперболе правее точки А, будут ближе к оси х, чем точка А, и, значит, на расстоянии, меньшем, чем 0,1. То же самое можно сказать обо всех точках гиперболы, находящихся левее точки В.

Ордината точки А равна 0,1. Найдем ее абсциссу, подставив это значение вместо переменной у в формулу. Она равна 50. Выбрав какое-нибудь значение абсциссы, большее 50, например 55, найдем точку с этой абсциссой, принадлежащую графику функции и удовлетворяющую нашему условию: , это точка с координатами .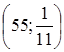

Поскольку в задаче требуется указать координаты какой-нибудь одной точки гиперболы, находящейся на расстоянии, меньшем, чем 0,1 от оси х, то ответ на вопрос уже получен. Однако, полезно заметить, что точка левой ветви гиперболы, симметричная найденной, – точка 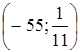также находится от оси х на расстоянии, меньшем 0,1. Число 55 было взято в качестве примера, очевидно, что ответы учащихся будут различаться. Для самопроверки полезно предложить учащимся указать расстояние от найденной ими точки до оси х и убедиться в том, что оно меньше 0,1. Так, в данном случае . Аналогичные рассуждения можно провести для расстояния, равного 0,01. Вполне возможно, что некоторые учащиеся будут решать эту задачу методом проб, подбирая требуемое значение х. Такое решение вполне допустимо, но все же полезно показать им и приведенное здесь

Формы и методы работы музея со старшеклассниками
Среди особенностей формирования личности в раннем юношеском возрасте следует выделить становление нравственного сознания, самосознания, чувство взрослости, стремление к самостоятельности в своей деятельности. Стремясь глубже разобраться в окружающей действительности, старшеклассники на многие вопро ...

Концепция университета
Средневековый университет несомненно был продуктом именно западноевропейской средневековой цивилизации. В определенном смысле его предшественниками были некоторые учебные заведения классической древности: философская школа в Афинах (4 в. до н. э.), школа права в Бейруте (3-6 вв.), императорский уни ...

Особенности обучения иностранному языку на старшей ступени обучения
Перед современной школой стоят задачи, связанные с созданием условий для интеллектуального и духовно-нравственного развития учащихся, для подготовки интеллигентного человека; для воспитания в каждом школьнике потребности в самообразовании, самовоспитании и саморазвитии; для формирования у учащихся ...