Методические рекомендации по изучению функциональной линии в 8 классе

№ 743.

Числа –3; 5; 0,5 являются нулями функции . Убедитесь в справедливости этого утверждения. Сформулируйте этот факт другими способами, используя слова «график», «значение функции», «уравнение».

Цель упражнения – в обучении переводу с одного языка на другой, умению выразить одно и то же утверждение разными способами. Убедиться в справедливости утверждения можно, подставив данные числа в формулу. Эквивалентные формулировки могут быть, например, такими: «график функции f(x) пересекает ось х в точках (–3; 0), (5; 0), (0,5; 0)», или «функция принимает значение, равное 0, при х, равном –3; 5; 0,5», или «числа –3; 5; 0,5 являются корнями уравнения ».

№ 746.

Начертите график какой-нибудь функции, нулями которой являются числа:

а)

–3,5; 0; 4;

б)

–5; –1; 2,5; 4,5.

Можно выполнять это задание парами – соседи по парте обменяются своими графиками, и каждый из них проконтролирует, правильно ли ответил на вопрос его напарник. Дополнить упражнение можно заданием: перечислить все свойства функции, которые можно выяснить по предложенному графику.

№ 752.

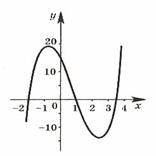
График какой функции изображён на рисунке 8?

,

,

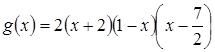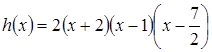, Рис. 8

.

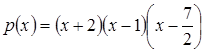Если использовать нули функций, то можно только отбросить функцию . Для остальных трёх нужно найти точку пересечения их графиков с осью у.

Работа сократится, если заранее заметить, что при подстановке нуля вместо х во вторую формулу получается отрицательное число и, значит, ордината точки пересечения соответствующего графика с осью у меньше нуля, а на предложенном графике она больше нуля. Остается выбрать из двух оставшихся функций h(x) и р(х).

График функции h(x) пересекает ось у в точке (0; 14), а р(х) – в точке (0; 7). Значит, на рисунке изображен график функции h(х).

В пятом пункте «Линейная функция» дано понятие линейной функции (функция, которую можно задать формулой вида y = kx + l, где k и l – некоторые числа, называется линейной) и её графика (графиком линейной функции является прямая).

Линейная функция – это первая конкретная функция, с которой знакомятся учащиеся. Так как учащиеся уже умеют строить график зависимости, заданной формулой у = kx + l (глава 4, пункты 4.1 и 4.2), то этот график служит опорой при введении всех понятий и свойств.

В ходе изучения данного пункта рассматривается большое число примеров реальных процессов и ситуаций, описываемых линейной функцией (в том числе и прямой пропорциональностью), поэтому учащиеся должны прийти к пониманию того, что величины разной природы могут быть связаны между собой зависимостью одного и того же вида. Это важно при формировании представлений о математическом моделировании, а также о практической значимости математических знаний.

Свойства линейной функции вводятся в пункте на основе конкретных графиков (расположение графика в координатных плоскостях, промежутки возрастания и убывания линейной функции). Учащиеся знакомятся еще с одним важным свойством линейной функции – описывать процессы, протекающие с постоянной скоростью.

Новой для учащихся является идея линейной аппроксимации, которая позволяет связать функциональный материал с вопросами статистики. На конкретных примерах, с опорой на графики, учащиеся знакомятся с зависимостями, которые не являются линейными, но приближенно могут быть заданы линейными функциями, что позволяет делать определенные прогнозы, получать приближенную числовую информацию.

Этот материал не является обязательным для усвоения всеми учащимися (не входит в обязательные результаты обучения) и в классах с невысокой математической подготовкой может быть опущен.

Формулирование выводов и оценка полученных результатов
Это результирующий (но не завершающий) этап исследования, когда делается то, ради чего задумывалось, организовывалось и проводилось исследование, происходит синтезирование всей информации, обобщение итогов всех видов ее анализа. Выводы исследователей призваны: * доказать истинность или ложность раб ...

Развитие связной речи в онтогенезе
В современных исследованиях в области лингвистики, психологии, педагогики выделяется разное количество этапов развития речи детей. Так, А.А. Леонтьев выделил: подготовительный (до 1 года), преддошкольный - этап первичного овладения языком (от 1 года до 3 лет), дошкольный (от 3 до 7 лет) и школьный ...

Методические рекомендации по разработке и применению кейс-методов
При разработке кейса можно выделить основные этапы создания кейсов: 1. Формирование дидактических целей кейса. Этот этап включает определение места кейса в структуре учебной дисциплины, определение того раздела дисциплины, которому посвящена данная ситуация; формулирование целей и задач; выявление ...