Этапы работы с площадями в средней школе

Тема "Площади фигур" изучается в школьном курсе математики в несколько этапов, а именно:

Пропедевтический курс (1-6 классы)

Основная школа (7-9 классы)

Старшая школа (10-11 классы)

В пропедевтическом курсе, который охватывает начальную школу и младшие классы среднего звена, учащиеся знакомятся с различными геометрическими фигурами, приобретают начальные навыки изображения этих фигур с помощью линейки, циркуля, угольника. С понятием площади учащиеся знакомятся на наглядно-интуитивном уровне. Школьники приобретают опыт непосредственного измерения, нахождения и сравнения площадей с помощью клетчатой бумаги, палетки, а также знакомятся с различными единицами измерения площадей и переводом из одних единиц измерения в другие.

На этом же этапе учащимся приводятся формулы для косвенного измерения площадей (формулы для вычисления площадей прямоугольника, квадрата, прямоугольного треугольника и круга), которые даются без всякого обоснования. Учащиеся вычисляют площадь прямоугольника, а также площадь фигуры, составленной из единичных квадратов.

Обязательным является умение решать задачи следующего типа:

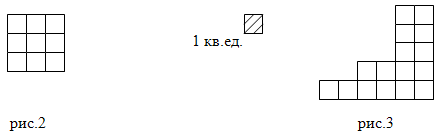
№ 1. Найдите площадь квадрата, изображенного на рис.2.

№ 2. Чему равна площадь фигуры, изображенной на рис.3.

№ 3. Длина прямоугольника равна 20 мм, ширина – 14 мм. Найдите площадь этого прямоугольника.

На втором этапе изучается большое число теоретических фактов, с помощью которых проводится опосредованное, косвенное измерение площадей. Переходя к этому этапу необходимо мотивировать для учащихся переход от прямого измерения площадей к косвенному, для чего полезно с ребятами вспомнить об инструментах, спомощью которых измеряются углы(транспортир), длины отрезков(линейка) и заметить, что нет такого удобного, точного инструмента, с помощью которого измеряются площади.

Измерение площадей начинается во всех учебниках с измерения площади прямоугольника. Для прямоугольника с длинами сторон, выражающимися целыми числами, формула S=ab легко устанавливается (она известна учащимся из курса начальной школы). В школьном курсе геометрии после изучения площади прямоугольника с длинами сторон, выражающимися целыми числами, в начальной школе (или, в крайнем случае, площади прямоугольника с длинами сторон, выражающимися конечными десятичными дробями) больше к вопросу о площади прямоугольника не возвращаются вплоть до изучения темы "Площадь многоугольников"(в 8-9 классах). При этом здесь формула площади прямоугольника S=ab считается известной (для любых прямоугольников) и с ее помощью выводятся формулы для вычисления площади треугольника и частных видов четырехугольников. Вычисление площадей многоугольников является составной частью решения задач на многогранники в курсе стереометрии. Поэтому основное внимание уделяется формированию практических навыков вычисления площадей многоугольников в ходе решения задач.

На этом же этапе доказывается формула площади круга: S= πr2 . Вывод этой формулы основан на теории пределов, которой в 9-летней школе нет. На интуитивном уровне учащиеся понимают, что периметр правильного многоугольника, вписанного в окружность, при неограниченном увеличении числа сторон и стремлении к нулю длины наибольшей его стороны "стремится" к длине окружности.

На данном этапе учащиеся решают несложные задачи на вычисление геометрических величин (длин, углов, площадей), применяя изученные свойства фигур и различные формулы и, главное, проводя аргументацию в ходе решения задач.

Обязательным является умение решать задачи следующего типа:

№ 1. Найдите площадь правильного треугольника, сторона которого равна 8 см.

№ 2. Найдите площадь прямоугольного треугольника, если его гипотенуза равна 17 см, а один из катетов равен 15 см.

№ 3. Диагональ квадрата равна 14 см. Найдите его площадь.

№ 4. ABCD – трапеция. Докажите, что треугольники ABD и ACD имеют равные площади (рис. 4).

№ 5. Найдите площадь круга, вписанного в правильный шестиугольник, сторона которого равна 4 см.

Значение театрализованной игры в жизни ребёнка
В педагогической литературе понятие «театрализованная игра» тесно смыкается с понятием «игра-драматизация». Одни ученые отождествляют эти понятия, другие считают игры-драматизации разновидностью сюжетно-ролевых игр. Так, по мнению Л.С. Фурминой, театрализованные игры – это нгры-представления, в кот ...

Выявление и оценка уровня сенсорного развития
Николаевой Т.В.была разработана методика комплексного педагогического обследования детей раннего и дошкольного возраста с нарушениями слуха. В этой методике представлены задания и для выявления и оценки уровня сенсорного развития Диагностика сенсорного развития предполагает выявление уровня развити ...

Этапы развития педагогики
Интенсивно развиваются, как самостоятельные, такие отрасли педагогической науки, как педагогика профтехобразования, педагогика высшей школы, военная педагогика, исправительно-трудовая педагогика. Складываются такие части педагогики, как школоведение, педагогика семейного воспитания, педагогика детс ...